レイトレ合宿9で4次元立方体をテーマにしたアニメーションを作成しました

CG, レイトレーシング, パストレーシング, OptiX, レイマーチング, CUDA, GPU, レイトレ合宿

9月1日(金)～9月3日(日)に日蓮宗大本山清澄寺で開催されたレイトレ合宿9に参加しました。

4次元空間上で回転してから、それを3次元に投影することで、内外が入れ替わるような不思議なループアニメーションをテーマにしました。

自作のレンダラーで 5分の制限時間 でレンダリングして4位をいただきました！次の動画は合宿運営側で制限時間内にレンダリングしたものです。

時間制限なしで4K解像度でレンダリングした動画はYouTubeにアップロードしました。

YouTubeの仕様の勉強も兼ねて、ループアニメーションという特性を活かしたYouTubeショート版も作成しました。

お寺で合宿！？

去年のレイトレ8は沖縄のラグジュアリーなホテルでの開催でしたが、今年は対照的に質素にお寺での開催でした。 運営メンバー曰く、ダイナミックレンジの広さを重視しているそうです！

去年のレポートはこちらです。

当日の詳細な様子については、@Kinakomoti2357さんのレポートがとても参考になります。 ぜひ合わせて読んでください。

本戦の実行環境

レイトレ合宿9の本戦では、AWSを利用してレンダラーを実行する必要があります。インスタンスタイプの選択肢は以下の通りです。

  • CPUレンダラーの場合: c6i.32xlargeを2台
  • GPUレンダラーの場合: g4dn.xlargeを2台（私はこちらを選択）

今年、新たなルールとして2台のインスタンスを利用できるようになりました。

私はフレームを半分に分割して2台のインスタンスを活用する単純な戦略にしました。 余談ですが、片方のインスタンスで描画が失敗してもバレないようにループは2周するようにしました（笑）。

毎年、新しい試みが取り入れられることが、この合宿の魅力の一つだと思います。

自作レンダラーの紹介

GPUレンダラーをOptiXで開発しました。レンダラーの名前はredflashです。

こちらがレンダラーのプレゼン資料です。

プレゼン資料をベースにしながら、当日話した内容などを文章として補足しながら紹介します。

アピールポイント

アピールポイント

アピールポイントは次の2点です。

  1. 4D上の回転を3Dに投影することで、内外が入れ替わる不思議なアニメーション
  2. 2023年に発表されたばかりのレイマーチングの高速化の論文を実装

基本機能

基本機能

レンダラーの基本機能です。

  • Unidirectional Path Tracing
    • implemented in NVIDIA® OptiX 6.5
  • Materials
    • Disney BRDF
    • Lambert Diffuse
  • NEE（Next Event Estimation）
  • MIS（Multiple Importance Sampling）
  • Primitives
    • Sphere
    • Mesh
    • Distance Function (Raymarching)
  • ACES Filmic Tone Mapping
  • Deep Learning Denoising

シンプルな単方向のパストレーシングで、NEEやMISサンプリングの効率化をしています。

OptiXのカスタムなプリミティブの衝突判定としてレイマーチングを実装し、距離関数によるプリミティブもサポートしています。 詳しくは過去の記事を参考にしてください。

余談ですが、昨今のレイトレ合宿では1フレームに使える時間が減っているのため、単方向のパストレーシングが多い印象でした。

レンダラーの出力設定

レンダラーの出力設定

レンダラーの出力設定について、解像度はフルHD（1920x1080）、長さはレギュレーション上の最大の10秒にしました。

30FPSで10秒なので、合計300フレームを描画しました。

制限時間が300秒（5分）なので、1フレームあたりに使える時間は1秒とかなり短めでしたが、ほとんどノイズが出ない綺麗な結果にできました。

超立方体（4次元上の回転）

レイトレ合宿で何を作ろうと考えた時、動画の最大の長さが10秒だったので、ループ可能なアニメーションが良さそうだと思いました。

ふと、TokyoDemoFest2021のShowdown準決勝でsp4ghetさんが表裏が裏返るようなアニメーションを作っていたのを思い出して、自分でもやってみました。

超立方体

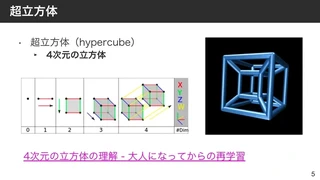
超立方体とは4次元空間上の立方体です。

4次元の回転を3次元から観測すると、内側と外側がグルグルと入れ替わるようなおもしろいアニメーションになります。

Tesseract

このアニメーションはWikipediaから引用しました。

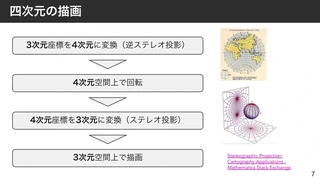
描画の流れ

具体的な実装としては、距離関数に与える座標をうまく加工しているだけです。

  • 3次元座標を4次元に変換（逆ステレオ投影）
  • 4次元空間上で回転
  • 4次元座標を3次元に変換（ステレオ投影）
  • 3次元空間上で描画

以下は、ステレオ投影とその利用例をCUDA C言語で実装したものになります。

実際の距離関数はマテリアル分けだったり、複数の距離関数を合成したりと、もう少し複雑になっていますが、分かりやすさ重視でシンプルにしました。

// 3次元座標を4次元に変換（逆ステレオ投影）
float4 inverseStereographic(float3 p)
{
    float k = 2.0 / (1.0 + dot(p, p));
    return make_float4(k * p, k - 1.0);
}

// 4次元座標を3次元に変換（ステレオ投影）
float3 stereographic(float4 p4)
{
    float k = 1.0 / (1.0 + p4.w);
    return k * make_float3(p4.x, p4.y, p4.z);
}

// 距離関数での利用例
float map(float3 pos)
{
    float f = length(pos);

    // 3Dから4Dに逆ステレオ投影
    float4 p4d = inverseStereographic(pos);

    // 4D空間のZW平面上の回転
    float2 p4d_zw = make_float2(p4d.z, p4d.w);
    rot(p4d_zw, (-time + 0.01) / 5 * TAU);
    p4d.z = p4d_zw.x;
    p4d.w = p4d_zw.y;

    // 4Dから3Dにステレオ変換
    float3 p = stereographic(p4d);

    // 3D上で距離関数を評価
    float d = dMenger(p / _MengerUniformScale0, _MengerOffset0, _MengerScale0, _MengerIteration0);
    d *= _MengerUniformScale0;

    // 空間の歪みを考慮して距離関数をスケール（0.7は係数）
    float e = length(p);
    d *= min(1.0, 0.7 / e) * max(1.0, f);

    return d;
}

4次元から3次元のステレオ投影の幾何学的な理解については、3Blue1Brownの動画にとても助けられました。

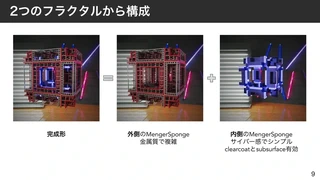
シーン構成

MengerSpongeと呼ばれる有名なフラクタルをベースにしました。外側と内側は2種類のMengerSpongeから構成されます。

外側と内側で対照的なマテリアルに設定していて、外側は複雑な金属感、内側はシンプルなサイバー感をイメージしました。

アニメーションの途中で部屋を暗くしていますが、サイバー感のあるマテリアルが光ってかっこよくなるように調整を試行錯誤しました。

モデリングの試行錯誤

モデリングはUnity上で行ってパラメーター調整してから、後からCUDAに移植するアプローチをとりました。

パラメーター調整はUnity上の方が作業しやすいからです。

レイマーチングの高速化

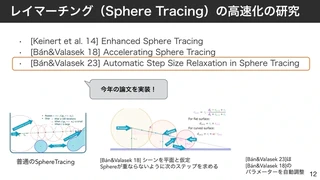
レイマーチング（Sphere Tracing）の高速化の研究

レイマーチングの高速化の論文を3つを調査しました。

  1. [Keinert et al. 14] Enhanced Sphere Tracing
  2. [Bán&Valasek 18] Accelerating Sphere Tracing
  3. [Bán&Valasek 23] Automatic Step Size Relaxation in Sphere Tracing

この3つの手法の基本的な考え方はどれも共通していて、通常より大きくレイを進めて、進み過ぎたら引き返すというシンプルなものです。

[Keinert et al. 14] Enhanced Sphere Tracing

[Keinert et al. 14] Enhanced Sphere Tracing

[Keinert et al. 14] では、レイのステップを $\omega \in[1,2)$ 倍して通常より大きくレイを進めます。

ω が小さいと効果が薄れてしまい、 ω が大きすぎると引き返しが発生して効率が悪くなります。

そのため、適切な ω はシーンの形状に応じて手動で調整する必要があります。

その他、この論文では「スクリーンスペースを考慮した交差点の選択」「自己交差を防ぐためのεの動的設定」「非連続性の緩和」「凸形状物質における最適化」にも触れられていますが、今回は割愛します。

[Bán&Valasek 18] Accelerating Sphere Tracing

[Bán&Valasek 18] Accelerating Sphere Tracing

[Bán&Valasek 18] は [Keinert et al. 14] の改良版で、レイを大きく進めるステップを定数ではなく状況に応じて計算します。

具体的にはシーンの形状を平面に仮定して次のステップを予測します。

  • マーチングループの現在のステップSphere（半径 $r_n$ ）
  • そのSphereに接する平面

上の2つにぴったり接する次のステップのSphere（半径 $r_{n+1}$）を決定し、ステップ $d_{n+1}$ を求めます。

さらに、シーンが平面でないカーブした面を考慮して、ωで調整できるようにします。

$$ d_{n+1} = r_n + \omega r_{n+1}, \omega \in(0,1) $$

[Bán&Valasek 23] Automatic Step Size Relaxation in Sphere Tracing

[Bán&Valasek 23] Automatic Step Size Relaxation in Sphere Tracing

[Bán&Valasek 23] は [Bán&Valasek 18] と同じ著者による研究で、平面を仮定する基本的なアプローチはそのままに ω を自動調整するようにさらに改良したものです。

  • 引き返しが起きない状態が続けばωを大きく
    • どのくらい大きくするかは $\beta \in(0,1)$ で調整
  • 引き返しが発生したらωをリセット

前の2つの手法より良いか同等の結果となっていました。基本アプローチは同じでパラメーター調整の工夫なので、納得できる結果です。

[Bán&Valasek 23] の結果

[Bán&Valasek 23] Automatic Step Size Relaxation in Sphere Tracingの結果

今回の提出シーンを使って、同じサンプリング数のレンダリング時間を計測したところ、約1.9倍ほど高速化しました（β=0.2）。

ここまで効果があるとは正直驚きでした。

[Bán&Valasek 23] Automatic Step Size Relaxation in Sphere Tracingの結果 時間ごと

時系列で見ていくと、歪みの少ないシーンほど効果が高く、歪みの大きいシーンは効果が少し下がるようでした。

この理由はシーンの形状に平面を仮定しているのが関係ありそうな気がしました。

[Bán&Valasek 23] Automatic Step Size Relaxation in Sphere Tracingの結果 Mandelbox

一方で去年のレイトレ合宿8のシーンで試したところ、むしろ性能が半分ほどに大きく劣化してしまいました。

Mandelboxというフラクタルのシーンだったのですが、平面が少なく、曲面で構成されるのが原因かもしれません。

まとめると、以下のような傾向がありそうでした。

  • MengerSpongeのように平面から構成されるフラクタルとは相性が良い
  • Mandelboxのように曲面から構成されるフラクタルとは相性が悪い

色んなシーンで検証したわけではないので、あくまで予想ですが、なんとなく納得はできる結果になりました。

セミナーの発表資料

45分枠をいただたので、2つのテーマ（20分＋25分）で発表しました。

Object Space Raymarching in Unreal Engine 5.2

レイトレ合宿アドベントカレンダーと同じ内容です。

Unreal Engine 5.2上でオブジェクトスペースのレイマーチングを実装したので、その解説をします。

レイマーチングをノードだけで実装するのは大変なので、MaterialのCustomノードを用いて複雑な処理はHLSLのコードで実装しました。

IFSによるフラクタルのモデリング

今回の合宿でも利用したMengerSpongeなどのフラクタルはIFS（Iterated Function System）と呼ばれる手法で距離関数を実装しています。

そのIFSについて、現実世界の実例（万華鏡や絞り染め）を用いて説明しました。

オススメのセミナー資料

どのセミナーもとても参考になる興味深い内容だったのですが、個人的に印象に残ったセミナーの資料を紹介します。

現代のGPUの実行スタイルとレイトレ (2023) by @Shocker_0x15

参加者投票によってベストプレゼンター賞にも輝いた @Shocker_0x15 さんによる「現代のGPUの実行スタイルとレイトレ (2023)」です。

「シェーダーではifが重い」という話はよく耳にしますが、これには古い情報や誤解が混ざっていることがあり、現代のGPUにおいては必ずしも正しいとは言えません。

現代のGPUにおいて、if文が性能にどのように影響するかを理解するためには、実行ダイバージェンスの観点からアプローチすることが重要です。 また、現代のGPUにおける命令実行戦略、データダイバージェンス、キャッシュとメモリの速度の違い、Occupancy（GPUのリソース利用率）、そしてレイトレーシングにおけるダイバージェンスの問題など、さまざまな要因が影響を与えます。

残念ながら、このようなトピックに関するまとまった日本語の資料は少ないため、この発表は非常に貴重なものでした。 シェーダーを扱う開発者は一度は目を通しておきたい発表でした！

[0.0, 1.0) の乱数を得るための“本当の”方法 by @h013

@h013さんによる「[0.0, 1.0) の乱数を得るための“本当の”方法」です。

[0.0, 1.0) のfloatの乱数を生成する方法は自明ではなく、ほとんどのC++標準ライブラリーの std::generate_canonical 実装では [0.0, 1.0) が保証されていないというのは驚きでした。

[0.0, 1.0) が保証される方法もパフォーマンス上の問題があったり、最適化の方法がさまざまに考案されていたり、こんなに乱数って奥が深かったんだと思いました。

これまで乱数について深く考えたことはなかったのですが、貴重な気づきが得られる発表でした。

Volume Expression GGX(Microfacet) by @Kinakomoti2357

@Kinakomoti2357さんによる「Volume Expression GGX(Microfacet)」です。

きなこもちさんはGGXは何処から来たのかという本を書いた方で、導入のMicrofacet BRDFの説明が分かりやすかったです。 レイトレを始めたばかりの人にもオススメできる内容でした。

個人的にMultiple-Scatteringの扱いについて気になっていたところだったので参考になりました。

本題のGGXのVolumeについても興味深い話だと思いました。

マテリアル神経衰弱

当日のレクリエーションとしてマテリアル神経衰弱が開催されました。

カード216枚もあり、ほとんど同じようなカードが多数存在するため、悪意を感じるような難易度の高さでした。

たとえば、同じ色でもplasticやphenolicなどの材質にバリエーションがあり、ほとんど同じにしか見えないが違うカードが多数ありました。

その難易度にもかかわらず、優勝チームはなんと3ペアを引き当てていました。すごすぎる…！

なお、カードはレイトレ合宿のためだけの特注品だそうです！

レクリエーションの内容は直前まで秘密にされていたため、合宿参加者は「一体何が起きるんだろう？」という気持ちで臨むことになりました。

感想

本戦は色々なアプローチに挑戦されている方が多く、多様性がありました。 1位のうしおさんはボクセル、2位のholeさんはボリュームなど、計算時間的に難易度な高そうなテーマを扱いながら、ノイズがまったく分からない結果だったので印象的でした。

去年に引き続き、セミナーは参加者全員で発表しました。参加者のバックグラウンドもさまざまだったので、いろんな分野の興味深い話や深い話を聞くことができて楽しかったです。

Yoshi’s DreannさんのSVGFやうでメガネさんのReSTIR PTなど、気になってはいるものの、なかなか手を出せていない手法についての発表も多く、自分も頑張らねばと思いました。

さまざまなグラフィックスAPIにおけるレイトレの話もありました。kugiさんのWebGPU、NishikiさんのVulkan、PentanさんのMetalなどです。

今年は新規の参加者も多かったので、色んな人とお話できるよい機会に恵まれました。

レイトレ合宿の運営の方々、その他の参加者のみなさん、本当にありがとうございました！

写真コーナー

レイトレ合宿史上初の寺での開催でした。開催地を聞かされた時、お寺で合宿が可能なんだ…という驚きが強かったです。

最終日は朝4時からお勤めあったり、3食とも精進料理だったりと、生活リズムが健康的になりました。いい経験になりました。

日の出もとても綺麗でした🌅

フリータイム中に境内を散歩したときの写真たちです。

CG, レイトレーシング, パストレーシング, OptiX, レイマーチング, CUDA, GPU, レイトレ合宿
comments powered by Disqus

gam0022.net's Tag Cloud

Recent Posts

最新記事

Read more

Books

ブログ執筆者の著書

Unityバイブル R5夏号
posted with ヨメレバ
kakunpc/室星 亮太/細田 翔/山本 剛史/小林 慶祐/長谷川 孝二 ボーンデジタル 2023年08月29日頃
楽天ブックスで購入
Amazonで購入
Kindleで購入
7netで購入
紀伊國屋書店で購入
図書館で探す
Unity ゲーム プログラミング・バイブル 2nd Generation
posted with ヨメレバ
森 哲哉/布留川 英一/西森 丈俊/車谷 勇人/一條 貴彰/打田 恭平 ボーンデジタル 2021年06月29日頃
楽天ブックスで購入
Amazonで購入
Kindleで購入
7netで購入
紀伊國屋書店で購入
図書館で探す