数値シュミレーションという授業で波動関数をシュミレーションする課題がありました。

面白かったので忘れないように、MathJax.rbというプラグインのテストを兼ねてメモすることにしました。

MathJax.rbの導入

MathJax.rbの導入には、30分のチュートリアルでJekyllを理解するが非常に参考になりました。

1. MathJax.rbをダウンロードして、/plugins/にコピーする。
2. octopressの場合、_layouts/layout.htmlではなくて、source/_includes/custom/head.htmlに次の行を追加する。

# source/_includes/custom/head.html
<script type="text/javascript" src="http://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML"></script>

MathJax.rbの使い方

ブロックの場合、mathとendmathタグで囲む

{% math %}

Simple\ FDTD\ Algorithm\ and\ Devils\ in\ the\ Details \\

\begin{eqnarray}
\psi(x,t + \Delta t) &=& -\psi(x, t - \Delta t) + [2 + \frac{v^2\Delta t^2}{\Delta x ^2} d_x^2] \psi(x,t) \\
$$ -\psi(x, t - \Delta t) + 2\psi(x,t) + \frac{v^2\Delta t^2}{\Delta x ^2} d_x^2 \psi(x,t) \\
$$ -\psi(x, t - \Delta t) + 2\psi(x,t) + \frac{v^2\Delta t^2}{\Delta x ^2}
                       [ \psi(x - \Delta x, t) + \psi(x + \Delta x, t) - 2 \psi(x, t) ] \\
\end{eqnarray}

{% endmath %}

インラインの場合、m とemタグで囲む(下のコードだと、emの部分が消えていますが囲んでください)

1次元の波を {% m %} \psi(x,t) {% em %} という

FDTD

私も詳細はちゃんと理解していませんが、1次元の波を $\psi(x,t)$ という 座標と時間をパラメータとした関数を使って表すとします。

このとき、FDTDというアルゴリズムを当てはまれば、漸化式によって波動関数をシュミレーションできます。

実際に計算してみると面白いと思います。

Simple FDTD Algorithm and Devils in the Details

$$\psi(x,t + \Delta t) $$ $$ = -\psi(x, t - \Delta t) + [2 + \frac{v^2\Delta t^2}{\Delta x ^2} d_x^2] \psi(x,t)$$ $$ = -\psi(x, t - \Delta t) + 2\psi(x,t) + \frac{v^2\Delta t^2}{\Delta x ^2} d_x^2 \psi(x,t) $$ $$ = -\psi(x, t - \Delta t) + 2\psi(x,t) + \frac{v^2\Delta t^2}{\Delta x ^2} [ \psi(x - \Delta x, t) + \psi(x + \Delta x, t) - 2 \psi(x, t) ] $$

FTDTでシュミレーションした例

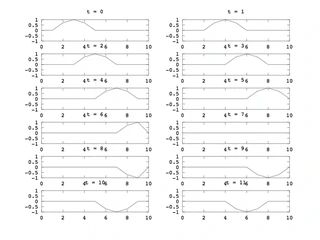
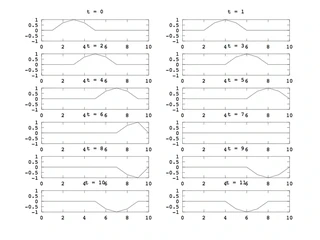
授業の課題の条件で計算したので、数字がとても荒いですが、FTDTで波動関数を計算した例を紹介します。

問題の条件はこれ。

$$\psi(0,0) = \psi(1,0) = 0, \psi(2,0) = sin(\frac{1}{4}\pi), \psi(3,0) = sin(\frac{2}{4}\pi), \psi(4,0) = sin(\frac{3}{4}\pi), \psi(j,0) = 0 for j = 5,6,..,10$$

$$\psi(0,1) = \psi(1,1) = \psi(2,1) = 0, \psi(3,1) = sin(\frac{1}{4}\pi), \psi(4,1) = sin(\frac{2}{4}\pi), \psi(5,1) = sin(\frac{3}{4}\pi), \psi(j,0) = 0 for j = 6,7,..,10$$

$$v = 1.0, \Delta x = 1, \Delta t = 1$$

条件を元に、FTDTの式を整理してみます。

$$\psi(x,t + \Delta t)$$ $$ = -\psi(x, t - \Delta t) + [2 + \frac{v^2(\Delta t)^2}{\Delta x ^2}d_x^2] \psi(x,t)$$ $$ = -\psi(x,t-1) + 2\psi(x,t) + d_x^2 \psi(x,t)$$ $$ = -\psi(x,t-1) + 2\psi(x,t) + \psi(x-1,t) + \psi(x+1,t) - 2\psi(x,t)$$ $$ = -\psi(x,t-1) + \psi(x-1,t) + \psi(x+1,t)$$

最終的に、こんなシンプルな漸化式になります。

$$ \psi(x,t) = -\psi(x,t-2) + \psi(x-1,t-1) + \psi(x+1,t-1) $$

上の式を元に計算すると、次のような波形を得られます。